位置エネルギーとは
別名ポテンシャルエネルギーとも言います。
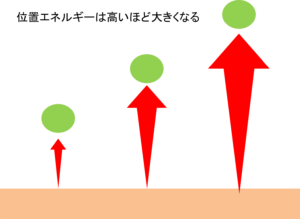
高さ h にある質量 m の物体が落下するときに、重力加速度を g とすると重力がこの物体に対して行う仕事は mgh となります=(質量×高さ×重力加速度)mgh を重力の位置エネルギーといいます。
要は物が落下するエネルギーだと考えれば簡単ですね。
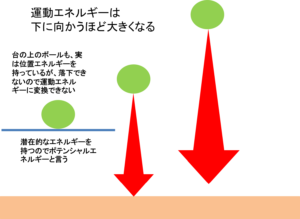

つまり人間の歩行や動作で例えるならば、Mst(ミッドスタンス)で高くなった重心は位置エネルギーが大きくなり、Tst(ターミナルスタンス)に向かって下降し始め運動エネルギーが大きくなる。そのため歩行で安定して速く歩くためにはミッドスタンスでの重心を出来るだけ高く保つ必要がある。
このときに重心を高く保つためには下肢の伸展機構と中殿筋などの外側支持機構が重要となる。
骨盤を水平に保ちつつ重心位置は高く保つ必要があるためです。またパッセンジャー(体幹)の伸展性も重心位置を決定するので重度の円背などでは十分な位置エネルギーは獲得できません。
次に落下する距離が大きくなければ運動エネルギーに変換出来ませんので、ある程度歩幅が必要となります。歩幅が小さければ重心の落下距離も小さくなるので加速が十分に出来ません。
イニシャルコンタクトの足関節の背屈はヒールでコンタクトするということで出来るだけ低い位置で足部を床へ接地させますので大きな落下加速度を得ることが出来ますね。
しかしそのまま落下するのでは重心の上下運動だけなので前方への推進力が生まれません。また衝撃が発生するので関節にもよくありません。
そのためロッカーファンクションにより踵の丸みによる前方への回転を利用して落下した運動エネルギーを前方に変換しています。
実に合理的ですね。しかもロッカーファンクションの起こるこのローディングレスポンスは衝撃緩衝作用があるので関節も痛めません。
位置エネルギー:
位置エネルギーを高くするためにミッドスタンスをしっかり作ること、運動エネルギーを大きくするために歩幅を大きくすること。
運動エネルギーを下方から前方に変換するためにイニシャルコンタクトの足関節背屈が重要であること。これが歩行時の位置エネルギーの役割です。
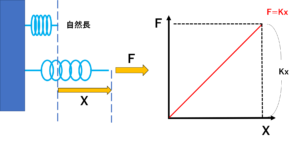
次に、ばね定数 k の線型ばねは正常な長さから x だけ伸ばす (または縮める) と正常な長さに戻ろうとするフックの力 kx が働き,正常な長さに戻るまでに他に対して1/2Kx²の仕事で戻ろとする力をバネの弾性の位置エネルギーといいます。
これはバネが元の位置に戻ろうとする力ですね。引き伸ばされれば戻ろうとしますし、圧縮しても戻ろうとしますね。この元に戻ろうとする力が弾性の位置エネルギーです。普段は単純に弾性エネルギーと呼んでいますね。
弾性エネルギー:
伸ばされた筋肉や腱は弾性力によって元の長さに戻ろうとします。また強く素早い伸長が得られれば伸張反射も発生しますので収縮局面に切り替わる瞬間(随意収縮)では通常の収縮力に反射による収縮力や上記の伸長によって蓄えられた弾性エネルギーが加わり普段よりも大きな収縮が得られます。
この様な収縮様式をプライオメトリクスと言います。ジャンプなどのダイナミックな運動にはこのプライオメトリクスが使われています。
また歩行時にもターミナルスタンス(Tst)での足関節背屈運動により、下腿三頭筋-アキレス腱に弾性エネルギーが蓄積され、プレスイング(Psw)で解放されることによって発揮されます。同時にステップ長(歩幅)が大きくなれば股関節伸展により腸腰筋や大腿直筋などにもこの弾性エネルギーが加わり通常歩行のアシストをします。このような伸長‐収縮サイクルをストレッチショートニングサイクル(stretch shortening cycle:SSC)と言います。
まとめ
重力の位置エネルギーは高いほど大きくなる。落下する力
弾性の位置エネルギーは伸ばすほど(縮めるほど)元に戻ろうとする力が大きくなる戻る力
理学療法では位置エネルギーといえば落下する力
弾性の位置エネルギーは弾性力と呼ぶ
歩行ではミッドスタンスを高くすることとイニシャルコンタクトを作ることで落下の最大距離を得られます。
また歩幅を大きくすることでSSCを使い省エネの歩行が可能となる。このそれぞれの力を利用することで人間は効率の良い歩行が可能となります。